Operations Research: VARIABLES IN INVENTORY PROBLEM #inventorymanagement #operationsresearch #production #bba #mba #ipumusings

VARIABLES IN INVENTORY PROBLEM

Operations Research: Inventory Management

We shall now proceed to classify the variables which are involved in an inventory problem.

The variables used in any inventory model are of two types:

1. Controlled variables,
2. Uncontrolled variables.

Controlled Variables :

The following are the variables that may be controlled separately or in combination :

The following are the variables that may be controlled separately or in combination :

1. How much quantity is acquired (by purchase, production, or some other means)?

This may be adjusted for each type of resources separately or for all terms collectively in one of the following ways:

1. The quantity to be ordered should be q quantity units;
2. The quantity to be ordered should be such as to stock level to S quantity units;
3. The quantity to be ordered should be such as to arise the stock level on hand and on order to z.
2. The frequency or timing of the acquisition. How often or when to replenish the inventory?

The inventory should be replenished when -

1. the amount in stock is equal to below S quantity units; or,
2. the amount in stock and the amount of order are equal to or below z. or,
3. at every t time unit.

The completion stage of stocked items.

More finished the goods, lesser the delay in meeting the demands. But, on the other hand, higher will be the cost of holding them in stock. Lesser finished the stock items, the longer the time in meeting the demands, consequently lesser the cost of holding in stock.
Most of the inventory models involve only the first two types of controlled variables.

Uncontrolled Variables :

The following are the principal variables that may not be controlled.

1. The holding costs (C₁), shortage or penalty costs (C₂), set-up costs (C₃).
2. Demand (the number of items required per period).

We note that it is not necessarily the amount sold, because some demand may go unfilled because of shortages or delays. It is in fact, the demand that would be sold if all that is required were available. The demand pattern of items may be either Deterministic or Probabilistic.
In the deterministic case, it is assumed that the quantities needed over subsequent periods of time are known exactly. Further, the known demand may be fixed or variable with time. Such demands are called static and dynamic respectively.
The probabilistic demand occurs when the demand over a certain period of time is not known with certainty, but its pattern can be described by a known probability distribution. A probabilistic demand may be either stationary or non-stationary over time.

3. Lead time (the time between placing an order and its arrival in stock.)

If the lead time is known and is not equal to zero, and if demand is deterministic, all that one requires to do is to order in advance by an amount of time equal to the lead time. While there is no need to order in advance if the lead time is zero.

If, however, the lead time is a variable that is known only probabilistically, the question of when to order is a more difficult one. If either the demand or the lead time is known only probabilistically, the amount and the timing of replenishment is found by considering expected costs of holding and shortage over the lead time required.

4. The amount delivered (supply of goods).

The supply of goods may be instantaneous or spread over a period of time. If a quantity q is ordered for the purchase of products, the amount delivered may vary around q with a known probability density function.

CLASSIFICATION OF CHARACTERISTICS OF INVENTORY SYSTEMS

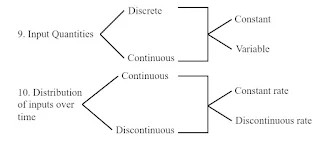
We may classify the characteristics of inventory problems as follows:

A LIST OF SYMBOLS FOR INVENTORY VARIABLES

The following symbols are generally used in connection with the inventory models:

C₁ = holding cost per quantity unit per unit time.
C₂ = shortage cost per quantity unit per unit time for the backlog case and per unit item only for no backlog case
C₃ = set-up cost per order
R = demand rate
K = production rate
t = scheduling time period which is not prescribed
t_v = to prescribed scheduling time period
x = demand during prescribed period t_v with probability F(x)
y = demand during lead time L with probability G(x)
z = order level (or stock level)
D = total demand
q = quantity already present in the beginning
L = lead time
f(x) = probability density function for demand x.

👉See Also:

What is Operations Research?
Different OR Models
Linear Programming - Formulation Technique (Q & A)
Linear Programming - Finding Graphical Solution
Costs Associated with Inventory Problems

Why inventory is maintained?